Several long runs have been done (and are being done) up to now. They require a massive simulation effort. We would like to report on the experimental behavior of HIDRA on several problems.
- Numerical integration of the motion of a spacecraft in the vicinity of the
libration points of the Earth-Moon system using a numerical model for the
full solar system (JPL ephemeris, all the planets plus the Moon). The
integrator used has been Runge-Kutta-Fehlberg of orders 7 and 8,
automatic step size control and maximum local relative error of 10-14.
HIDRA is able to compute the motion of the spacecraft at an average rate of
more than 12 years per second.
-
Computation of Lyapunov exponents and rotation number of a second order linear
differential equation with quasiperiodic coefficients (ref.: Broer, H.,
Simó, C.: ``Hill's equation with quasi-periodic forcing: resonance tongues,
instability pockets and global phenomena'', Bulletin of the
Brazilian Mathematical Society, in press).
A systematic and massive computation of Lyapunov exponents in that simple problem allows to understand some key points in the reducibility problem for quasiperiodic coefficients and in the breakdown of tori. HIDRA allows to compute the time 2p-map at a rate of more than 5,000,000 iterates per second. See figure 1 for the resonance tongues and the line of tori breakdown.
-
Interactive computation of Poincaré sections, invariant manifolds, bifurcation
diagrams, etc.
Many dynamical systems have to be simulated in an interactive way to gain insight on the dynamical properties. HIDRA allows to obtain between 104 and 105 Poincaré iterates (through a suitable transversal section) per second on simple ordinary differential equations of moderate dimension (say, between 3 and 7). This high performance allows quick interactive explorations. An invariant manifold like the one whose section is displayed in figure 2, related to the unfolding of a codimension 3 bifurcation, is computed by HIDRA in 5 seconds.
In all the computations mentioned above the sustained output has been, at least, 2 Gflops, reaching 2.7 Gflops in processes with low rates of transfer of data. (September, 1998).
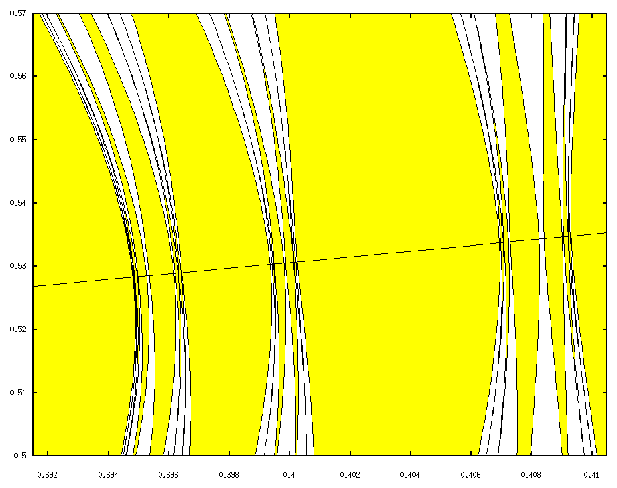
Figure 1: Resonance tongues and line of collapse of resonances, where the breakdown of tori occurs.
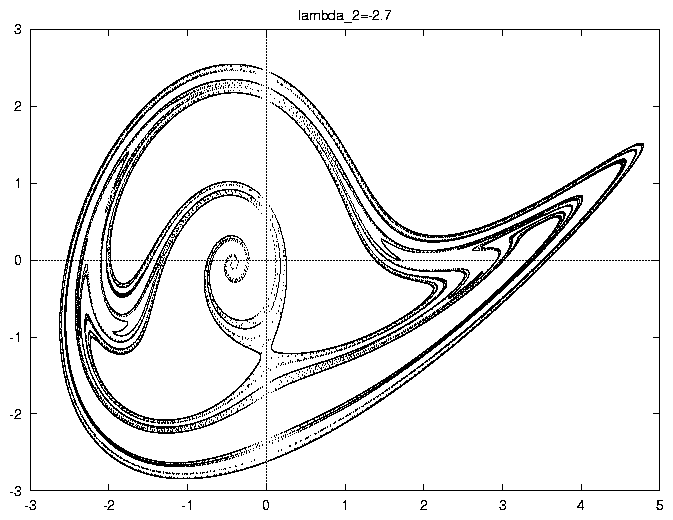
Figure 2: Section of a 2D invariant unstable manifold of a 3D system.