HIDRA: A HOME-ASSEMBLED PARALLEL COMPUTER


Presentation
HIDRA is a parallel computer obtained by linking together several
Pentium-based PCs, by means of a dedicated network (this is usually
known as
Beowulf-class computer).
The hardware used is:
- 1 PC with 2 Pentium Pro 200 processors (master node).
- 12 PCs with 2 Pentium II 266 processors each.
Every PC has 128 Mbytes of RAM and IDE hard disks of 3.2 Gbytes.
They are linked together by
a 100 Mbits Ethernet network (with two hubs). The master node
acts as a gateway between the
network of the Department and the HIDRA internal network.
We have used Linux (Slackware 3.4, kernel 2.0.33) on each node, and we
use the public domain version of the PVM and MPI message passing
libraries for the communications.
The initial benchmarks show a sustained performance of 2 Gigaflop in
several applications we are interested in (simulations of some
dynamical systems),
but it seems that it could deliver 3 times this
performance using very specific (and useless!) benchmarks.
The Barcelona UB-UPC Dynamical Systems
Group works, among other things, on several projects that require
a huge amount of computations (i.e., numerical simulations of
continuous and discrete systems, bifurcation analysis,
numeric and symbolic computation of
invariant manifolds, etc.). In this context, HIDRA is a very good
solution for our computing necessities since many of the algorithms we
use can be parallelized very efficiently.
The computing needs of the Group
Most of the research projects involve Dynamical Systems (discrete and
continuous, parametric studies, bifurcation analysis, computation of
invariant manifolds, etc, both numerically and symbolically).
Symbolic computations with ad hoc manipulators including up to several
millions of terms and arbitrary precision long tasks are also done.
Typically a project can require up to 10^15 elementary arithmetic
operations. Systems of low dimension (e.g., the number of variables and
parameters is at most 6 or 7) are analyzed exhaustively to obtain a
description of the phase space as complete as possible. Higher
dimensions are only analyzed partially. All the related software is
developed, analyzed and implemented by members of the Group.
A Beowulf cluster seems to be a good solution to satisfy these needs. It
consists of
- A pile of PC,
- A dedicated network connecting them,
- A communications software
- A software allowing to start/stop processes and to pass data from one
processor to another.
This is the basic configuration of HIDRA, as described above.
Programming tasks for this parallel machine is easy. The conversion from
a program running on a sequential computer to a parallel one is simple if
the program is structured as a main code calling many times some
computing routine and avoiding unnecessary data transmission. Anyway
an effort is required to investigate if alternative algorithm, may be
not efficient on a sequential computer, can have a higher performance on
a parallel one. In any case, to have a good performance, a detailed
analysis and comparison of algorithms is essential.
A presentation demo is described below. All times refer to "clock"
times, as estimated manually. Almost all of them have an important part
of graphics, in contrasts with the usual tasks of the Group, where
graphics play a role for presentation just at the end of a long
computation. No effort has been made to optimize graphic routines.
- The unavoidable computation of the Mandelbrot set for quadratic
complex maps. A test using 1600 x 1200 pixels in the black region of the
set, where computations are stopped after 2560 iterates, takes 25
seconds. The number of operations for iteration (including tests!) is
10. This gives an average performance close to 2 Gflop/s.
Click on the figure to see a sequence of 6 magnifications with resolution
800x800 pixels each. The first one is 35K large.

- Computation of the prime numbers between 1 and 2^31-1 using a Fortran
program. A sieve method is used. Typically a variable for each number
is set to 1, then the multiples of primes 2,3,5,...,46337 (larger than
those primes) are set to 0. Finally the variables are examined to see
the ones which remain equal to 1. These are the primes. The cost is:
a) to put to 1, b) to cancel (the sum of the inverses of the above
primes is close to 2.64), c) to scan the list. Every step requires to
move an index and to set or look for a number. The total estimated cost
is 2(2+2.64)(2^31-1)=19.93 Giga. The clock time for the run is 10
seconds.
Click here to see two figures about prime number
density.
- Computation of basins of attraction for the Newton method when
looking for the roots of a (complex) polynomial in a domain of the
complex plane. Each pixel is set to a color depending on the root to
which it converges. All computation are done in real*8 variables. If the
degree of the polynomial is n, the computation cost of each Newton
iterate an scan for the proximity to one of the roots is 16(n+1). For
the program use is made of the knowledge of the roots (computed at the
beginning) to speed up the task. The total cost depends strongly of the
polynomial and on the domain. A run for a degree 32 polynomial on a
suitable square domain of size 10^(-10) around a preimage of a critical
point requires in total 1.124E8 iterates of Newton method. The computing
(and displaying) time is of 27 seconds, giving an average performance of
2.2 Gflop/s.
Click on the figure for a 800x800 magnification (39K).

- Computation of the phase portrait on a Poincaré section of the
classical Hénon-Heiles cubic potential in two degrees of freedom on the
level of energy h=0.12. For each of 250 initial points 4000 iterates
have been computed. A Taylor method of order 24, with derivatives
obtained by recurrent use of Leibnitz method has shown to be very
efficient. The effort of each integration step is, roughly, 3000 operations. A
total of 4.6E9 steps is required and the total computing time is 23
seconds. The accuracy of the integration is measured by the maximal
change of the energy for initial energies in (0,1/6) and a scan of the
Poincaré section for the initial point. In all cases it is below 2E-16.
Note that the "classical" order 4 Runge-Kutta method gives, in the best
case, an error 30 times larger with a computing time also 30 times
larger. Computations with the same cost display errors of 3E-9. Even the
better RKF78 method is only able to reduce the figure 30 to 3 in both
places and with the same cost produces error up to 3E-11. Here we attain
2 Gflop/s.
Click on the figure for a 784x784 magnification (105K).

- Computation of the rotation number for the quadratic Hénon
conservative area preserving map for different initial values of the
distance to the elliptic fixed point and different values of the
parameter. The rotation number is simply estimated by "counting
revolutions" (of course, we use typically more efficient methods, but
this is a demo!). Each iterate requires 10 operations (including
tests for revolution and eventual escape). A run with 100 values of the
parameter, 400 distances for every value of the parameter and 100,000
iterates (provided they do not escape)
per point requires, in total, 2.7E10 iterates. It takes a
computing time of 13.5 seconds, with an average performance of 2
Gflop/s.
- The motion around one of the collinear points of the spatial circular
restricted three-body problem is unstable. However this is a nice place
for spacecraft missions. Several missions have already been launched
(ISEE-3 and SOHO). Many other are planned. Their orbits lie on the
"center manifold" of the collinear points. This manifold can be
approximated by symbolic computation to any desired order, and the
Hamiltonian can be reduced to this manifold, skipping in this way the
instability in the computations. This reduction has been performed by a
previous program (up to order 46) and the demo just takes the degree 6
approximation of
the Hamiltonian. It contains 55 terms. A computation with 75 initial
points and 1000 iterates per point, on a suitable Poincaré section takes
53 seconds.
Click on the figure for a 850x680 magnification (45K).
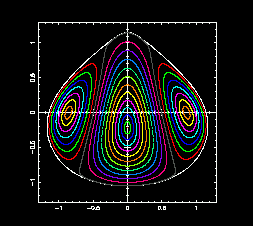
- A more realistic computation is done using the full solar system
(i.e. Sun, planets and Moon) to study the stability zones around the
triangular libration points of the Earth-Moon system. JPL ephemeris are
used and this requires the computation of the positions of all these
bodies by a Chebyshev interpolation polynomial on a suitable time
interval (which changes from body to body). Then Newton equations of
motion are integrated, to determine the evolution of a massless particle,
by using a RKF78 algorithm. The average global number of integration
steps delivered by HIDRA is 30,000 steps/second.
Summary
HIDRA is a very efficient tool for most of the computing tasks we
undertake.
Difficulties: It can require an effort to obtain the most suitable
algorithms to improve the performance. Problems in high dimension (e.g.,
numerical solution of partial differential equations) would benefit from
shared memory or a much faster communication.
Advantages: Beyond the know how we have developed, this is a tool to
solve problems and, also, a source of theoretical and practical
problems. From another point of view is fully scalable, updatable and
recyclable.
Future: It is planned to increase the number of nodes to 24, to
increase the amount of RAM memory of each PC, to update gradually the
nodes to faster processors, depending on the best available
performance/price, and to increase the communications hardware if this
shows to be a bottle neck for some problems.
Acknowledgments
The construction of HIDRA has been made possible thanks to grants of the
Spanish Ministry of Culture and Education, the Generalitat de Catalunya
and the support of the University of Barcelona.
We specially want to thank the people around the Linux, GNU and PVM projects,
for putting in the public domain such a good software. Without them,
this would have been only a dream (or a nightmare? :-)).
Barcelona, march 25th 1998.
Joaquim Font, Àngel Jorba,
Carles Simó, Jaume Timoneda (click here
for a picture)


 Back to the UB-UPC DSG home page
Back to the UB-UPC DSG home page









